H8.dvi
8.2 It has been hypothesized that silicone breast implants cause illness. In one study it was foundthat women with implants were more likely to smoke, to be heavy drinkers, to use hair dye, andto have had an abortion than were women in a comparison group who did not have implants. Usethe language of statistics to explain why this study casts doubt on the claim that implants causeillness. Sol

 Chapter 22 One-Way Analysis of Variance: Comparing Several Means
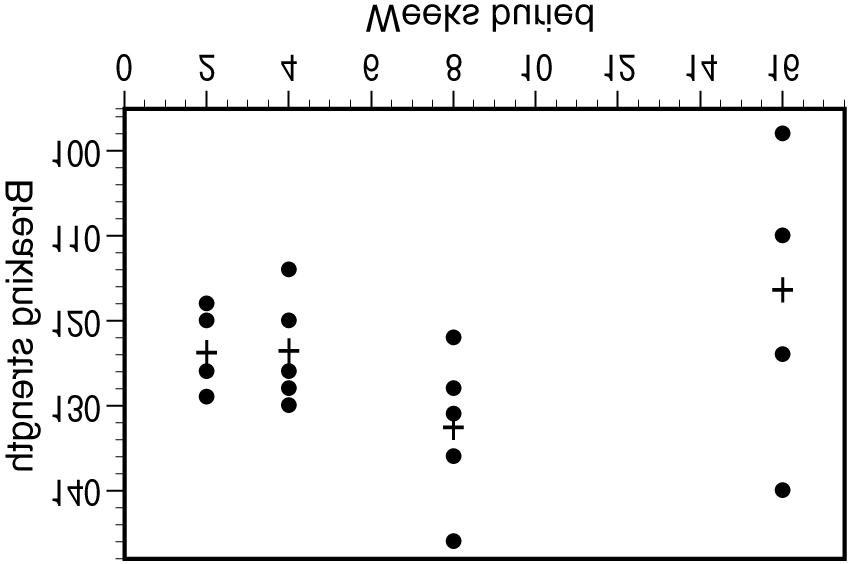
22.20. (a) We test H0: µ1 = µ2 = µ3 = µ4 = µ5 vs. Ha: not all means are the same. (b) N = 168, I = 5,
Chapter 22 One-Way Analysis of Variance: Comparing Several Means
22.20. (a) We test H0: µ1 = µ2 = µ3 = µ4 = µ5 vs. Ha: not all means are the same. (b) N = 168, I = 5,